Price:
5831 EUR
Contact
Massachusetts Institute of Technology
Description
Differential equations are the language of the models that we use to describe the world around us. In this series, we will explore temperature, spring systems, circuits, population growth, biological cell motion, and much more to illustrate how differential equations can be used to model nearly everything.
We will develop the mathematical tools needed to solve linear differential equations, understand 2x2 systems of first-order linear and nonlinear differential equations. We will use linear algebra to solve systems of more than two differential equations. As well as, explore the use of Fourier series to analyze the behavior of and solve ordinary differential equations (ODEs) and separable partial differential equations (PDEs). In the last course of the series, we will consider frequency domain and Laplace transform to help us appreciate their effects on mechanical and electrical systems.
Learner Testimonials
"Wonderful course on differential equations. The teachers provide a nice computational tool to depict the dynamics of solving the equations, which is very useful for students to grasp the key ideas and concepts.” - Jiting (completed this course, spending 10 hours a week on it and found the course difficulty to be medium)
"Interesting course. Lectures, homeworks and review exercises of any part are really well setup. One of the best MOOC on topic of differential equations." - Gaetano (completed this course, spending 4 hours a week on it and found the course difficulty to be medium)
"Another excellent course from MIT. The lecture videos are excellent and so are the exercises. This course also has MATLAB based exercises which is wonderful. The problem sets are excellent and so are the staff and the community teaching assistants who are always there to help any time." - Dna47a (completed this course, spending 8 hours a week on it and found the course difficulty to be medium)
Specific details
Category of Education
Physical Science

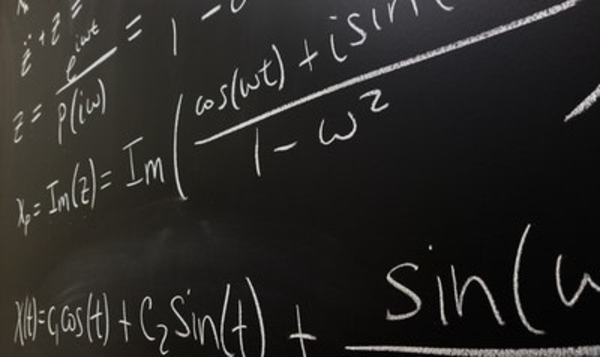





 How to resolve AdBlock issue?
How to resolve AdBlock issue? 


Comments (0)